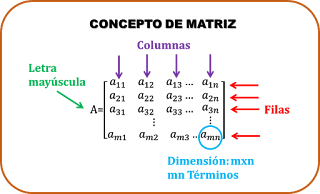
La notación matricial, propiamente dicha, fue utilizaba por primera vez por Cayley en 1843, quien desarrolló el álgebra de matrices (suma y producto, matriz unidad, matriz inversa de otra …), aunque el nombre de matriz fue acuñado por su gran amigo Sylvester en 1850.
Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Además de su utilidad para el estudio de sistemas de ecuaciones lineales, las matrices aparecen de forma natural en geometría, estadística, economía, informática, física, etc...
La utilización de matrices (arrays) constituye actualmente una parte esencial de los lenguajes de programación, ya que la mayoría de los datos se introducen en los ordenadores como tablas organizadas en filas y columnas : hojas de cálculo, bases de datos,...
El dominio del álgebra matricial es fundamental para afrontar con éxito otros temas de este curso, que utilizan las matrices como herramienta, entre los que podemos citar, por ejemplo: determinantes, resolución de sistemas de ecuaciones lineales.
En este tema se verán los conceptos que considero más relevantes para el EBAU, como son los conceptos de matriz y sus distintos tipos, las operaciones de matrices y la matriz inversa (método directo y Gauss-Jordan) y aplicaciones de las matrices a la vida real. El rango de una matriz en principio no entra y de los determinantes sólo lo más básico que es calcularlos por la regla de Sarrus.
- Resumen de la teoría de las Matrices y de Determinantes
- Esquema de las matrices
- NEW apuntes de Matrices y determinantes (23-9-18)
- Apuntes de Matrices Web IES Aricel y ejercicios resueltos y sin resolver.
- Apuntes de Determinantes Web IES Aricel y ejercicios resueltos y sin resolver.
+ INFO (RECURSOS de MATRICES y DETERMINANTES)- Coleccion de ejercicios de Matrices Web matematicasonline I , II y III
- Web Vitutor con apuntes de Matrices y Determinantes
- Web tuprofedematesonline con teoria y videos explicativos (Matrices y Determinantes)
- Proyecto Descartes sobre las matrices
- NEW Colección de Ejercicios Sistemas de Ecuaciones Matriciales (1-10-18)
- NEW Interpretación de Matrices (Ejercicios con solución) (6-10-18)
Aquí dejaré algunos videos explicativos sobre las matrices y sus operaciones.- Colección de videos explicativos de Unicoos (nivel alto)
- Matrices nomenclatura y tipos
- Operaciones con matrices
- Producto de matrices
- Potencia de matrices
- Rango de matrices por Gauss 01
- Rango de matrices por Gauss 02
- Matriz inversa Gauss-Jordan
- Matriz inversa Gauss-Jordan 2
- NEW Sistemas de Ecuaciones Matriciales (1-10-18)
CALCULADORA ONLINE DE MATRICES
Con esta aplicación web podrás calcular determinantes (por la regla de Sarrus o haciendo ceros en la fila o columna que queramos), rangos, hacer una suma (o resta) de matrices, producto de matrices, calcular la matriz inversa, resolver sistemas de ecuaciones por Cramer, por Gauss-Jordan, eliminación gausiana, aplicar el teoema de Rouché–Frobenius, etc. Todo lo que vemos en clase y más cosas.
Una calculadora de matrices es un software que nos permite a los estudiantes calcular matrices inversas, producto de matrices, suma de matrices, etc. de una manera rápida y sencilla evitando el largo trabajo de realizar estas operaciones en hoja y lápiz.
0 comentarios:
Publicar un comentario