La Estadística descriptiva y la teoría de la Probabilidad van a ser los
pilares de un nuevo procedimiento (Estadística Inferencial) con los que
se va a estudiar el comportamiento global de un fenómeno. La
probabilidad y los modelos de distribución junto con las técnicas
descriptivas, constituyen la base de una nueva forma de interpretar la
información suministrada por una parcela de la realidad que interesa
investigar.
 El impacto inicial para el planteamiento de las matemáticas de la teoría de la probabilidad provino de la investigación de los juegos de azar durante el renacimiento. se puede localizar los fundamentos de probabilidad hacia la mitad del siglo XVII, en la correspondencia intercambiada por el matemático Pascal y el jugador Chevalier de Mere estos desarrollo y otro elaborados por por matemáticos bernoulli, demoiure y Gauss los percusores de la materia de la inferencia estadística. sin embargo no ha sido hasta principio en este siglo que estadística como pearson, fisher, gosset,neyman, wald y tukey iniciaron el desarrollo de los métodos inferencial de la estadística, los cuales tienen muy amplia aplicación en diversas de campo en la actualidad
El impacto inicial para el planteamiento de las matemáticas de la teoría de la probabilidad provino de la investigación de los juegos de azar durante el renacimiento. se puede localizar los fundamentos de probabilidad hacia la mitad del siglo XVII, en la correspondencia intercambiada por el matemático Pascal y el jugador Chevalier de Mere estos desarrollo y otro elaborados por por matemáticos bernoulli, demoiure y Gauss los percusores de la materia de la inferencia estadística. sin embargo no ha sido hasta principio en este siglo que estadística como pearson, fisher, gosset,neyman, wald y tukey iniciaron el desarrollo de los métodos inferencial de la estadística, los cuales tienen muy amplia aplicación en diversas de campo en la actualidad
La estadística Inferencial es una parte de la estadística que comprende los métodos y procedimientos que por medio de la inducción determina propiedades de una población estadística, a partir de una pequeña parte de la misma. La estadística inferencial comprende como aspectos importantes:
- La toma de muestras o muestreo, que se refiriere a la forma adecuada de considerar una muestra que permita obtener conclusiones estadísticamente válidas y significativas.
- La estimación de parámetros o variables estadísticas, que permite estimar valores poblacionales a partir de muestras de mucho menor tamaño.
- El contraste de hipótesis, que permite decidir si dos muestras son estadísticamente diferentes, si un determinado procedimiento tiene un efecto estadístico signifivativo, etc.


- Resumen de la teoría de las Variables aleatorias y de la Inferencia estadística
- Apuntes a mano de estadística I , II y III
- Web IES Aricel (muy interesante)
- Web con teoría y ejercicios de Inferencia estadística (vitutor)
- Web explicando la teoría de muestras
- Web explicando los conceptos de Intervalos de Confianza
- Página con otra forma de ver la teoría
- Teoría Estadística (son varias secciones)
- Coleccion de Ejercicios de Intervalos de Confianza
- (NEW) Colección de Ejercicios Andalucia 2017
- Distribucion Normal Tipificada N(0,1) | Tipificacion (FisicayMates) Recomendable
- Distribucion Normal 01 BACHILLERATO Selectividad Tipificar (unicoos)
- Distribucion Normal 02 BACHILLERATO Selectividad (unicoos)
- Intervalo de confianza BACHILLERATO Distribucion Normal matematicas (unicoos)
- Tamaño de una muestra BACHILLERATO Distribucion Normal (unicoos)
- Coleccion de videos explicativos de la Inferencia Estadistica (FisicayMates) Recomendable.
- Listado de videos con Estadística: distribuciones muestrales, binomial y normal

















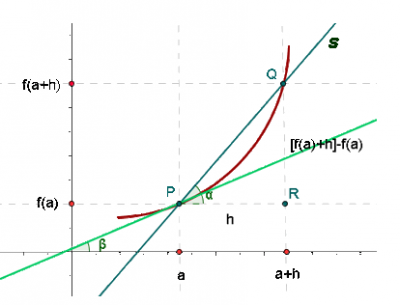
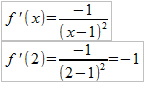
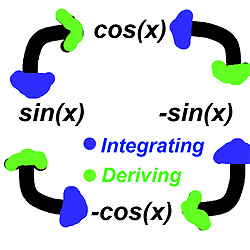
 + INFO (RECURSOS de DERIVADAS y APLICACIONES)
+ INFO (RECURSOS de DERIVADAS y APLICACIONES)